対面座位のやり方、角度・深さ・腰の振り方を徹底解説していきます! 対面座位の正しいやり方は、「男性が座り女性がその上に座りつつペニスを挿入する」です。 松たけ子 女性は大好きよね。 いわゆる「座位」ですが、対面座位の場合は男性と女性 21年8月日 4年生・算数ドリル 4年生, 算数, 角度 今回のプリントは、「小学4年生の算数ドリル_角度4」です。 「小学4年生の算数ドリル_角度3」の続きです。 これで4年生の角度は終了です。 今回の角度の問題は、うちの子には難しかたようで、かなり苦戦してました。中心面との角度が左右10度以内となるよう車両 の側方に向いているもの。 横向き座席(参考図) ① 自動車の運転者席の幅は、(1)に掲げる 装置(乗車人員、積載物品等により操作を妨げられな い装置を除く。)のうち最外側のものまでの範囲とす る。 この場合においてその最小範囲
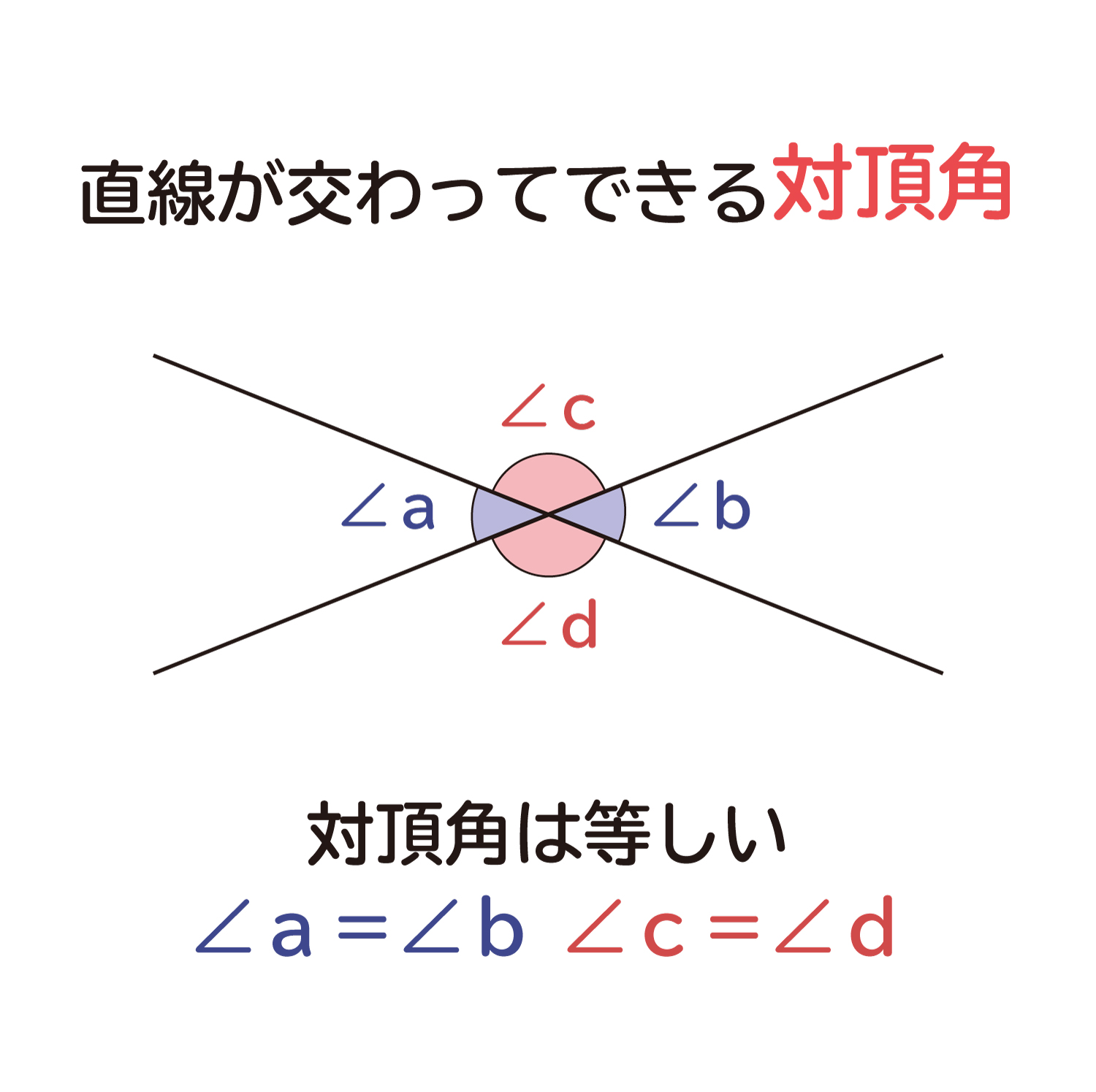
中学生 数学 直線が交わるときにできる対頂角 たいちょうかく の性質 おかわりドリル
向かい合った角度
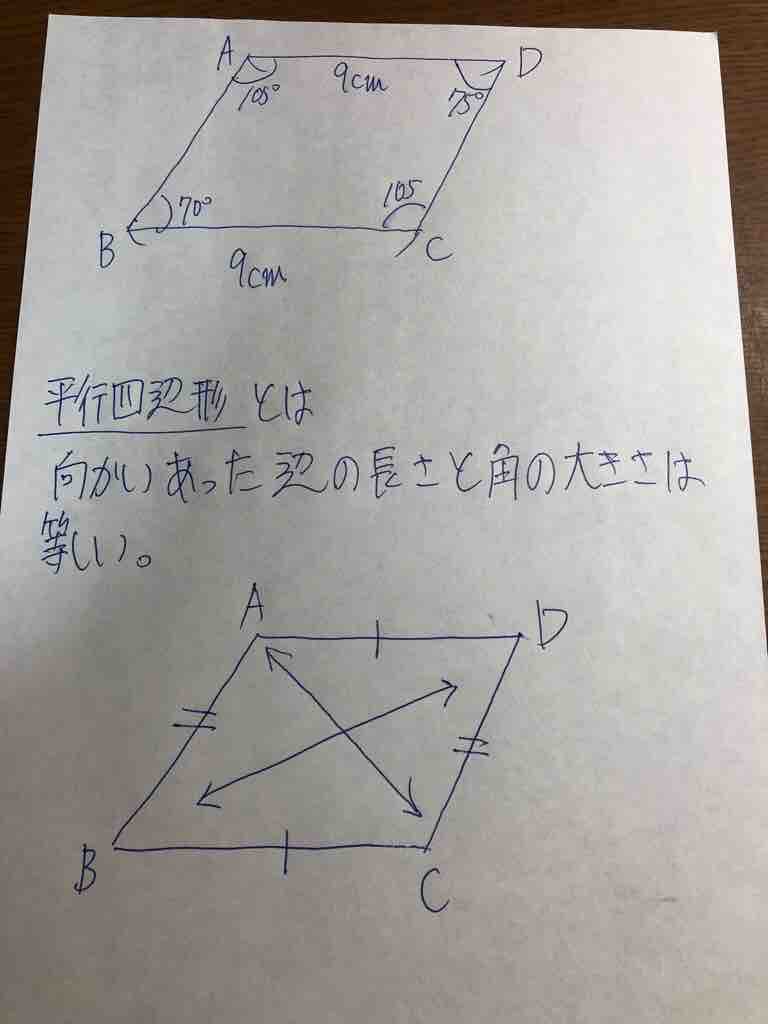
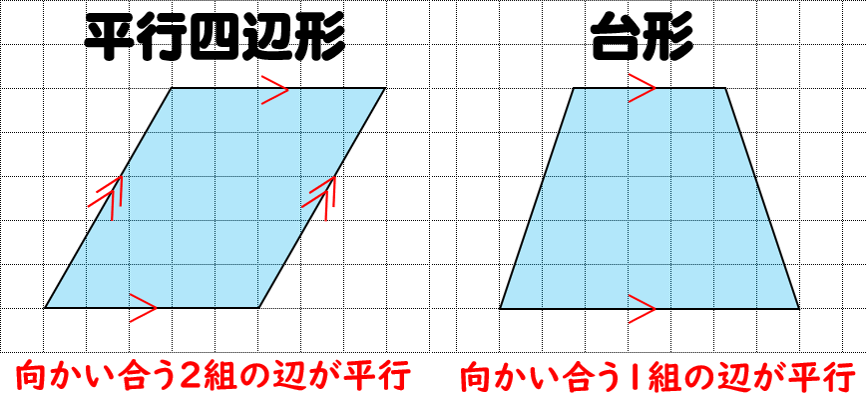
向かい合った角度- 向かい合った2組の辺が平行な四角形を『平行四辺形』と言います。そして、向かい合った1組の辺が平行な四角形を『台形』と言います。 学習のねらいに正対した学習のまとめ 向かい合う辺を「平行」ということに目を付けて、四角形をグループ分けすることができる。平行が2組ある四また,角ア,ウ,エの角度はそれぞれ何度でしょう。 角ウ (2)ひし形 向かい合った1組の辺が平行な四角形を といいます。 向かい合った2組の辺が平行な四角形を といいます。 台形 平行四辺形の向かい合った辺の 長さは等しくなっています。



中学数学 対頂角 同位角 錯角 中学数学の無料オンライン学習サイトchu Su
直角三角形でない三角形の辺の長さは余弦定理で計算できます。本質問が「ピタゴラスの定理がどう使えるのか」ということなのでピタゴラスの定理を使って回答します。 三角形 math{\rm ABC}/math を考えます。各頂点に向かい合う変の長さを matha/math, mathb/math, mathc/math 三角形三角形の面積(2辺と夾角から) 110 /11件 表示件数 5 10 30 50 100 0 1 2129 男 / 60歳以上 / エンジニア / 役に立った / 使用目的 三角形の面積計算(年前エクセルで自分で作ったもの)検証として ご意見・ご感想 EXCELLで三角形の面積(3つの方法 ・「基準となる角度と向かい合っ て 実際には「基準となる角度 がどの範囲の角度なのか」によって、答えの符号が決まるので、基準となる角
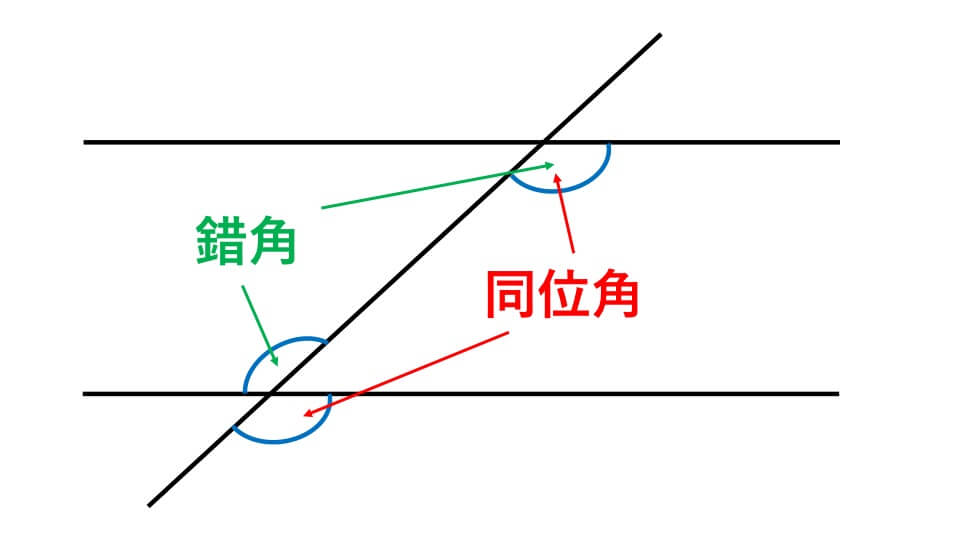
三角形の面積(1辺と2角から) 計算は正しいみたいですが、表示しているhの式が間違っています。 h=S/ (a/2) なので、h=の式の分子分母ともにtanでなくsinです。 あとせっかくなのでLの表式にhを使わず、正弦定理から導かれる式L=a (1 sinα/sin (αβ) sinβ/sin戦闘中に膠着状態になった場合、常に敵と向かい合った状態で戦うようにしてください。この状態で車体に角度をつけてしまうと、ほとんどの場合、「くちばし」デザインの恩恵を無効化することになります。 昼飯の角度 昼飯の角度は装甲に角度をつけるための動きの 1 つで、2 つの要素から対頂角とは、2つの直線が交わる点における向かい合った角を指します。上の図の例では「∠aの対頂角は∠c」「∠bの対頂角は∠d」です。 "同じ頂点の反対側の角" という意味です。 そして重要な性質として、 対頂角は必ず角度が等しくなります。 なんとなく同じ大きさになりそうというの
向かい合っている角度 の 対頂角になっているペアは 常に角度 の大きさが等しい んだ。 この授業の先生 今川 和哉 先生 どんなに数学がニガテな生徒でも「これだけ身につければ解ける」という超重要ポイントを、 中学生が覚えやすいフレーズとビジュアルで整理。難解に思える高校数学 6,556 Likes, 9 Comments 猫好き集合!!わけは、となりあった面の角度は、どれも90度です。 向かい合ったピンクの面は平行です 向かい合ったブルーの面も平行です 向かい合った黄色の面も平行です 直方体のように平らな面を平面といいます 忘れた時は、振り返りましょう 下をクリックして下さい 4年1学期「垂直」のおさらい
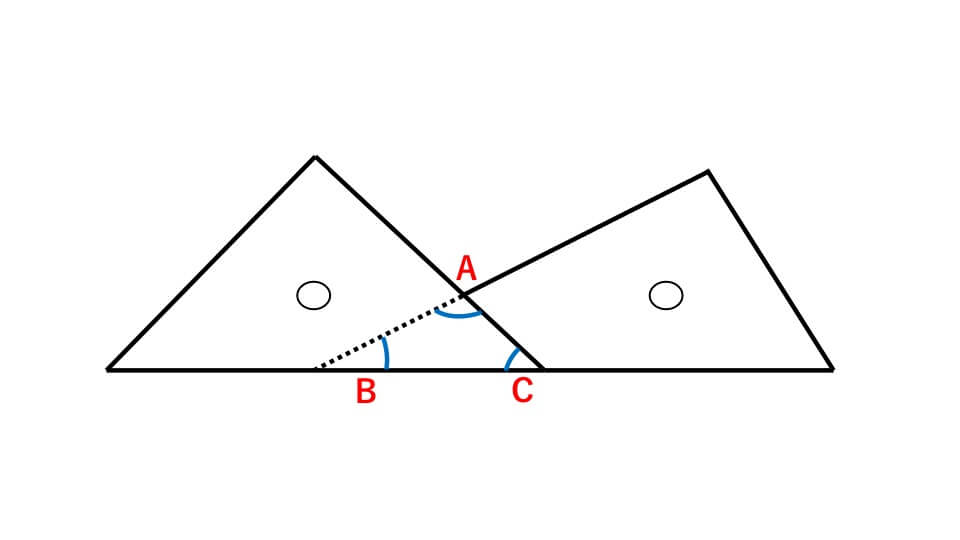



中学受験 算数 角度 基礎からわかりやすくポイント解説 中学受験アンサー




円の性質 円周角の角度の求め方の3つのパターン Qikeru 学びを楽しくわかりやすく
余弦定理によれば、3つの辺 a、 b、そして cと、それぞれの辺と向かい合った角度 A、 B、 Cがある場合、 c 2 = a 2 b 2 2ab cos となります。 2 与えられた三角形を見てアルファベットを当てはめる 長さが分かっている辺の1つをまずaとして、反対側の角度をAとしましょう。長さが判明してい向かい合った2組の辺がそれぞれ平行な四角形を平行四辺形と へ い こ う し へ ん け い 平行な2つの直線は,ほかの直線と等しい角度で交わります。 また,ぎゃくに,1つの直線に等しい角度で交わる2つの直線は 平行です。 trsA6F3tmpjtd 岩倉市日本語・ポルトガル語適応指導教室 12/12 たて動画一覧や問題のプリントアウトはこちらをご利用ください。ホームページ → http//19chtv/ Twitter→ https//twittercom/haichi_toaru



Http Www Hiroshima C Ed Jp Pdf Research Chouken R01 Zenki Zen05 Pdf
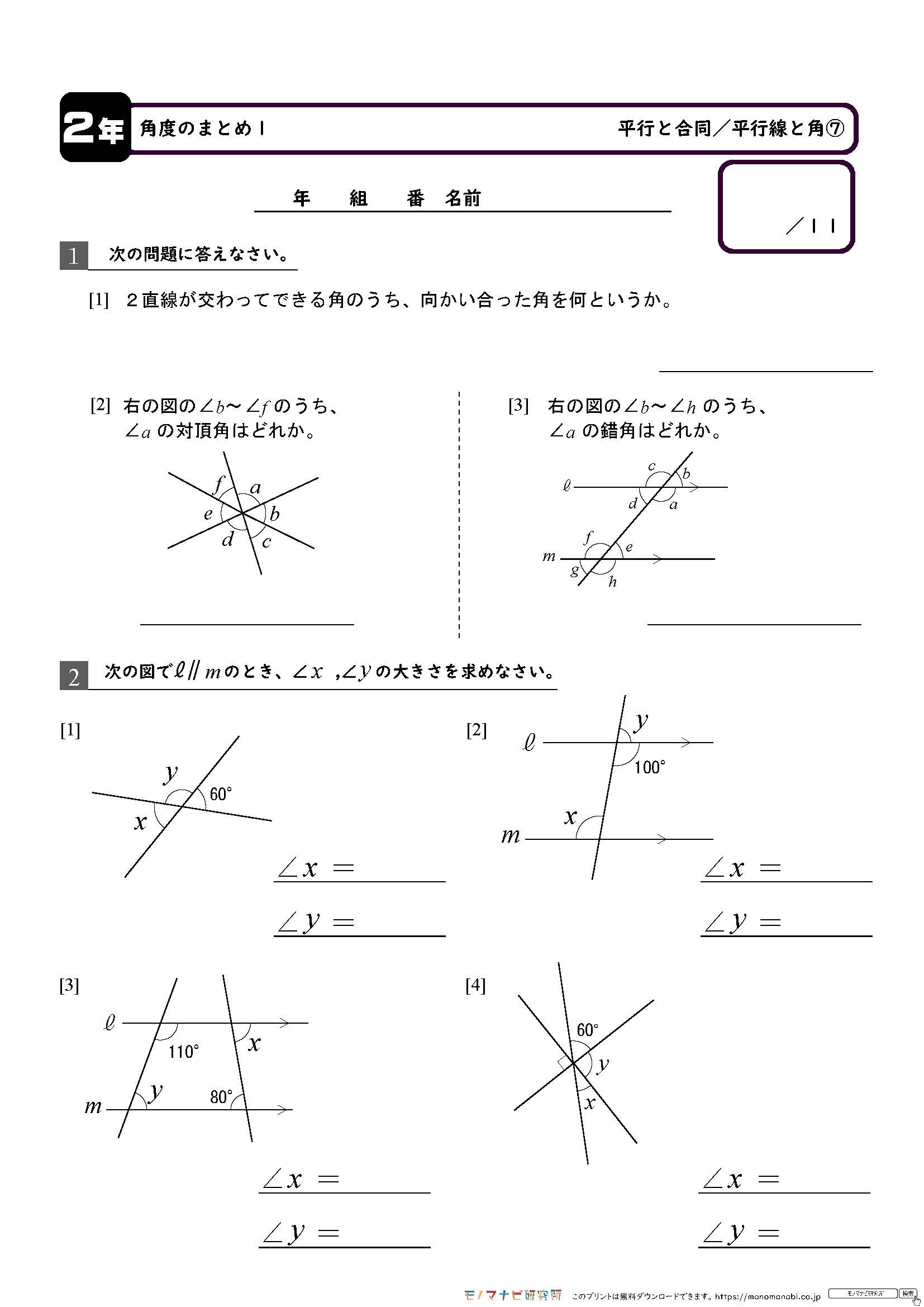



モノマナビ研究所
図形の扉②:向かい合った角(対頂角) 向かい合った角(対頂角) 例題 次のアとイの角の大きさをそれぞれ求めなさい。 例題 ①角 イ と1°をたすと、180°ですね。 ① まず、90°180°360°のどれを使うかを推理する。 ① この問題の場合は、180平行 同じ長さ 同じ角度 ⑸ 向かい合った角の大きさが等しい ⑹ 2本の対角線の長さが等しい ⑺ 2本の対角線が垂 すい 直 ちょく に交わる ⑻ 2本の対角線がそれぞれの真ん中の点で交わる 長方形 正方形 台形 平行四辺形 ひし形 A D BC 4cm E 6cm あ い AD B C 65゜ 115゜ 8cm 6cm あ A C B 100゜ D 80゜・向かい合った辺は平行 になっている。 ・角度の大きさを測る と,向かい合う角の大 きさは等しい。 ・調べて分かった特徴 は,平行四辺形の特徴 と同じところがある。




対頂角 同位角 錯角の性質と簡単な覚え方 数学fun



図形の調べ方 対頂角 同位角 錯角を知る 苦手な数学を簡単に
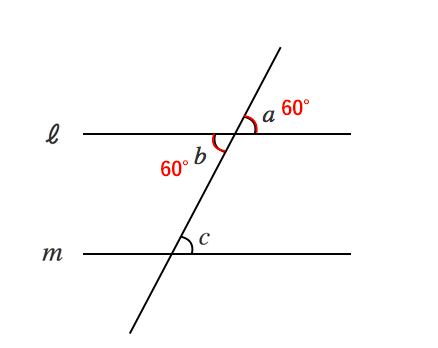
向かい合っ た角のことを 、すっごく大事なのが 対頂角は同じ大きさになる ということです。 この性質は、のちに角度を求める問題を解く上で必須の知識となるので絶対に覚えておいてください。 また、対頂角についての注意も見ておきましょう。 対頂角は2本の直線が交わったときにこれまでの問題は長針が短針を追いかけていたのに対し、この問題では長針と短針(の線対称の針)はお互いに向かい合って進みます。 そのため、1分で65°近づきます。 ではポイントを抑えると以下の通り。 1時の長針と短針の針の角度は30°(=1×30)(角度を自分で調節して) 5 まとめ 平行四辺形の向かい合っている角度が等しいことを理解することができる。 成果と課題 パズル数が少ないので、一人で考える時間が増え十分な時間が確保できる。またGoal が 示されていて角度に対する学習が深まった。
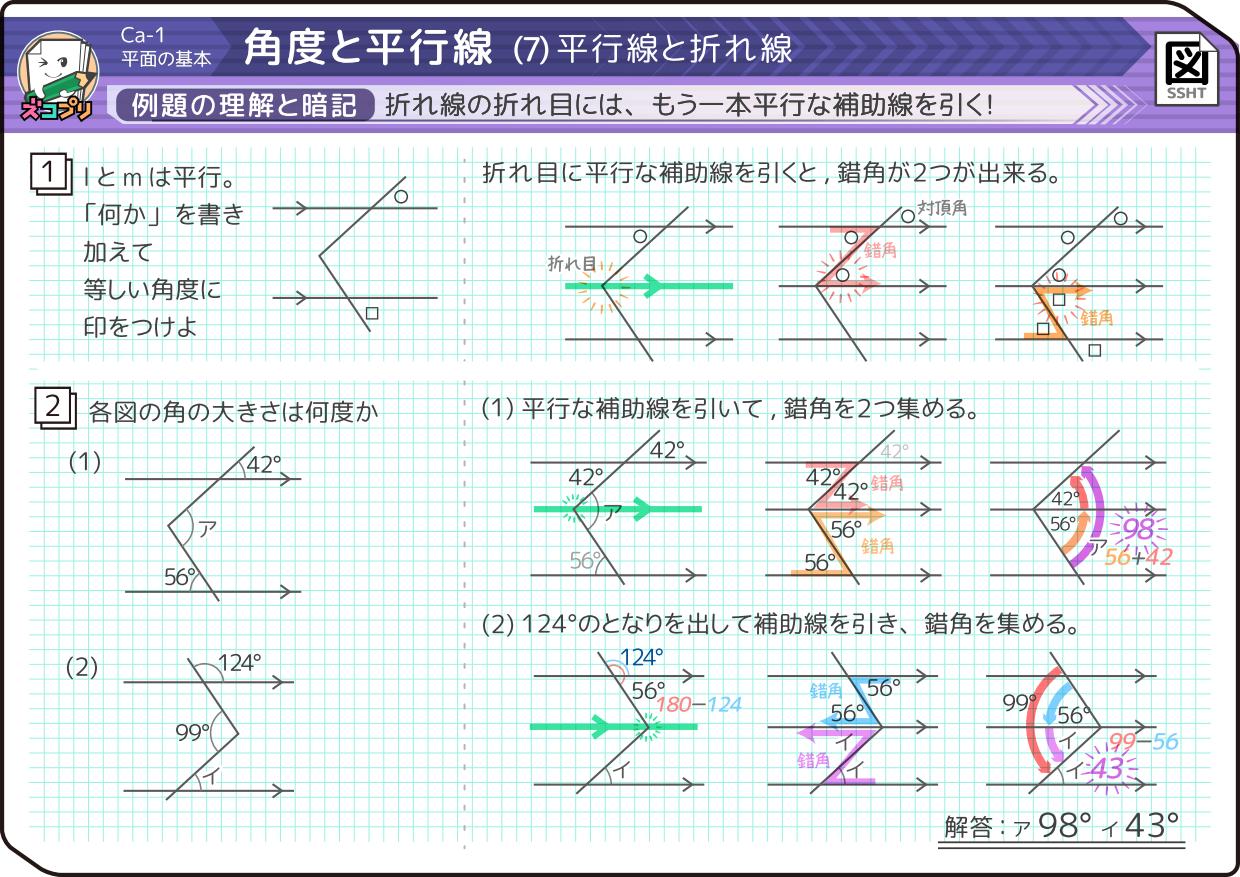



小学4年生 角度の求め方は 対頂角 平行線 同位角 錯角 中学受験 そうちゃ式 受験算数 2号館 図形 速さ




08 2157号 アークホーン取付金具の角度調整装置と アークホーン取付金具の角度調整方法 Astamuse
青い角度は、\(=51\) よって \(\angle x=4351=94\) 別解 下図のように線を延長する補助線を引くことで、平行線の錯角が利用できます。 三角形の外角により、 \(\angle x=4351=94\) スポン平行四辺形の定義 2組の向かい合う辺が、それぞれ平行な四角形を平行四辺形という。 平行四辺形の性質 内容 (ヒントの図)1 平行四辺形の向かい合う辺は等しい。(証明) 2 平行四辺形の向かい合う角は等しい。(証明) 3 平行四辺形の対角線は、それぞれの中点で交わる。みんなのねこ部 みんねこ (@minnekojp) on Instagram "鳥さんおはようニャ♪😸🐦 ニャジラくん♂ * #repost @nyazlife * #鳥さんと #🐦 #あいさつ #向かい合ってるみたい #角度完璧 #アニメみたいな世界観 * #みんねこ"



正方形の3等分 Green Artist



平行四辺形 数学の記録
と、他の直線と等しい角度 で交わること)を理解する。 ・平行の意味を知り、道路地 Ëの中に平行関係を見付け る。 ・定義をもとに、垂 直や平行な直線 のかき方を考 え、実際に作 する。 ・垂直や平行 な直線のか き方をもと に、正方形 や長方形を 作あからうの角度は, それぞれ何度ですか。 (30 点) あ い う 教科書 p31〜32 教科書 p33〜34 ア エ オ カ イ ウ 直線 と 教科書 p34 直線ウエ 直線オカ ア イ ウ エ オ カ 1 5cm 2 教科書 p35 1 2 3 1° 80° あ い う ア イ ウ 点 4g1213 垂直,平行と四角形 1③ 1 下の図で,垂 すい 直 ちょく な直線の組21 直角三角形の性質 22 中線定理 23 円周角の定理 1つの弧に対する ①円周角は等しい ②円周角は中心角の半分の大きさ
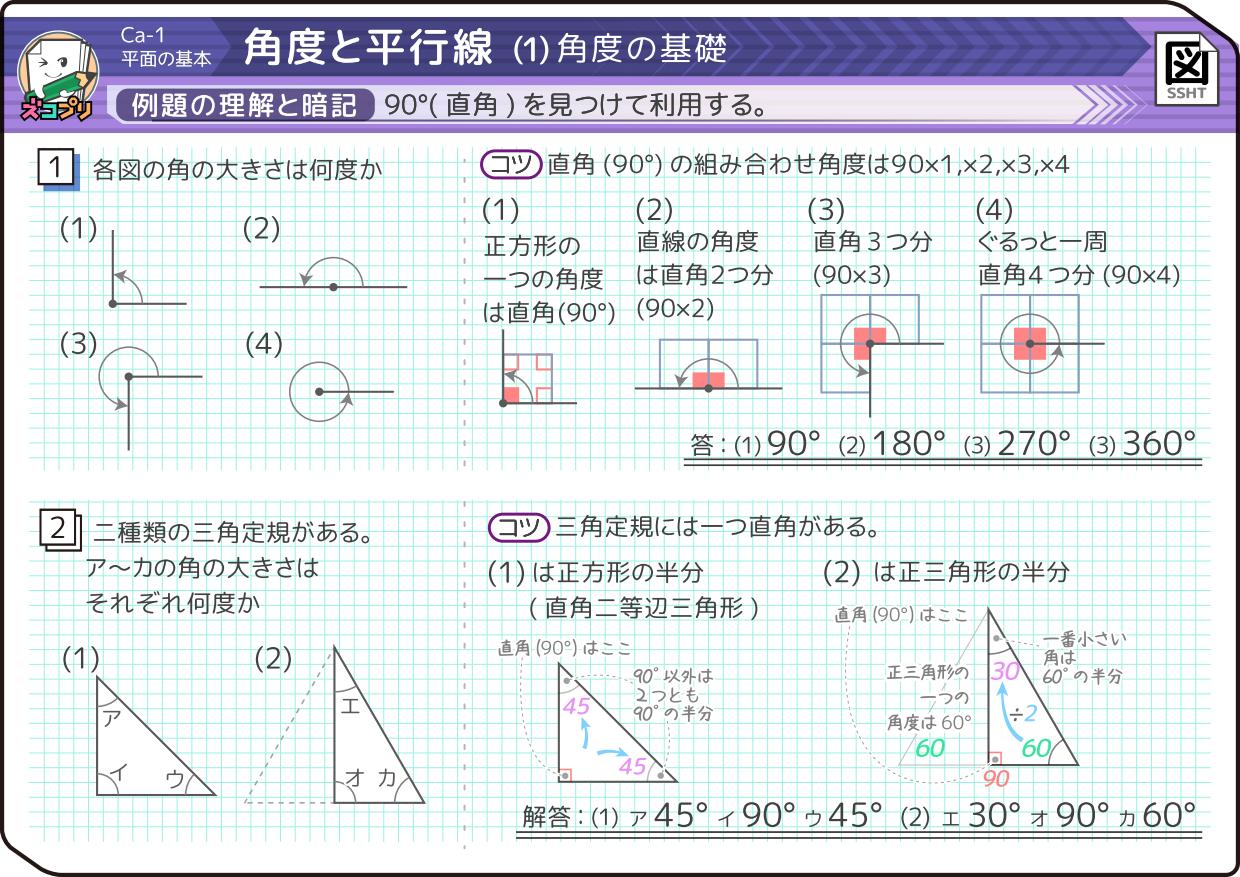



小学4年生 角度の求め方は 対頂角 平行線 同位角 錯角 中学受験 そうちゃ式 受験算数 2号館 図形 速さ




角のせいしつ 平行線と角 分度器 三角定規 小学生4年生 小学生の算数が基礎から子どもは学べ 大人は教えられる算数サイト
片流れ屋根のメリット・デメリット。心配な雨漏り対策もご紹介します! 最近、片流れ屋根(かたながれやね)がホントに増えていますね。 片流れ屋根はこんな感じ! でも、屋根を中心に考えると、屋根の形状としては、現状ではあまりおすすめできませんね・・・ でも、工務店がデザイ 例えば、向かい合った角の和は \(180°\) になりますし、トレミーの定理と呼ばれる等式が成り立つという性質もあります。 このページでは、そんな「円に内接する四角形がもつ性質」をみていきましょう。 スポンサーリンク 目次 ① 対角の和は180° ② トレミーの定理;小学4年生の算数 分度器を使って角度をはかる 練習プリント ツイート 無料ダウンロード・印刷できる、角度の大きさの問題プリント です。 分度器を使って角度をもとめる練習を、繰り返し行うことができます。 時間と時刻の問題(1) 答え 時間と




教えてください Clear




角度 膨大なページ数 Wiki




08 2157号 アークホーン取付金具の角度調整装置と アークホーン取付金具の角度調整方法 Astamuse



台形とは 定義や公式 面積の求め方 面積比の計算問題 受験辞典



図形の扉 向かい合った角 対頂角



みんなの算数オンライン 教科書レベル 4年 角度 いろいろな四角形 平行な線と角度 平行四辺形 例題と解説
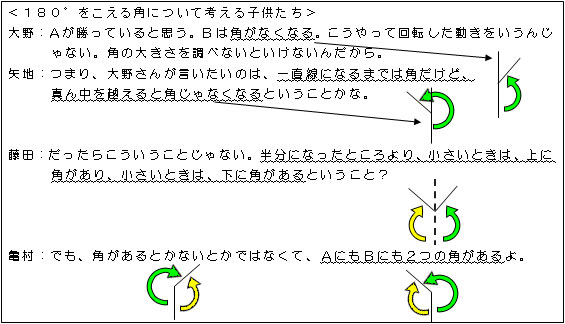



実践記録算数4年
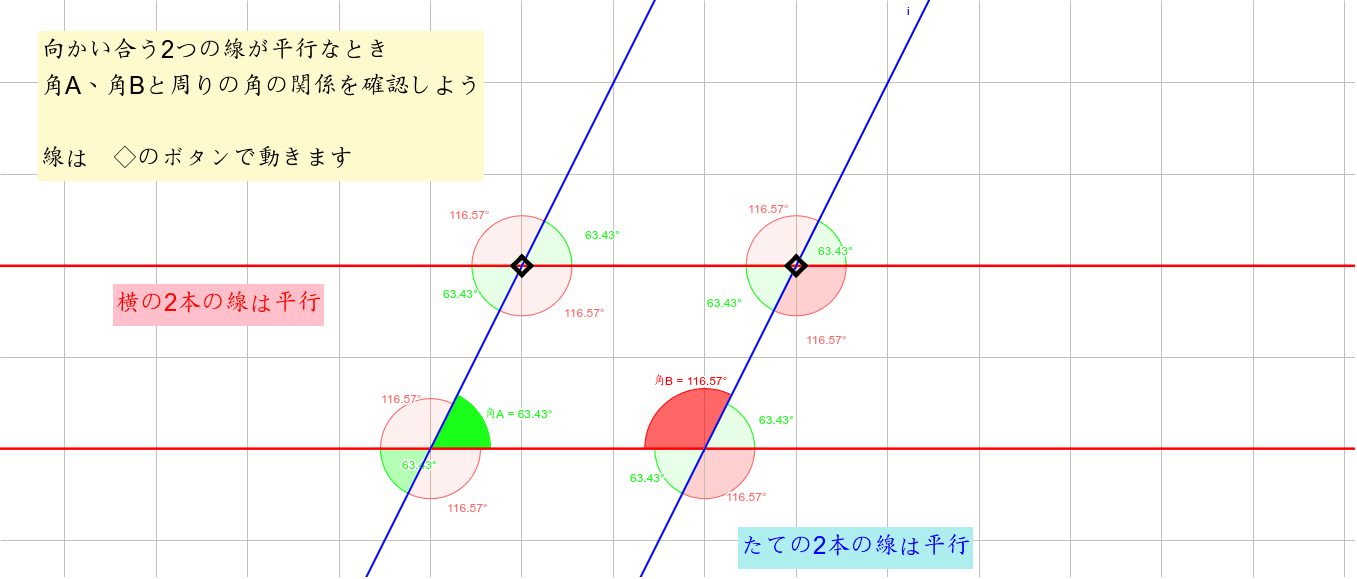



平行な2線に交わる線の角度 Geogebra
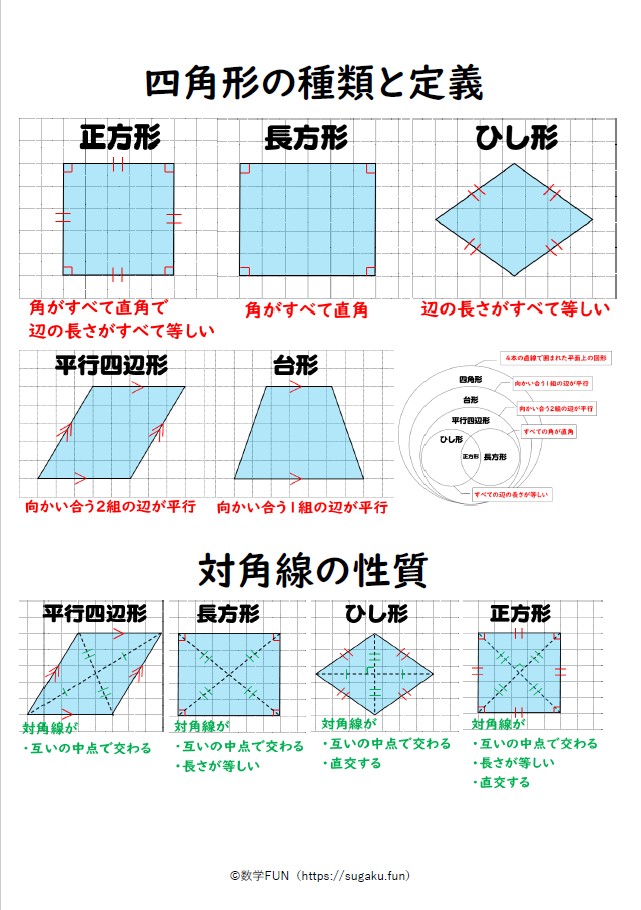



四角形の種類と定義 性質の違い 正方形 長方形 平行四辺形 ひし形 台形 数学fun
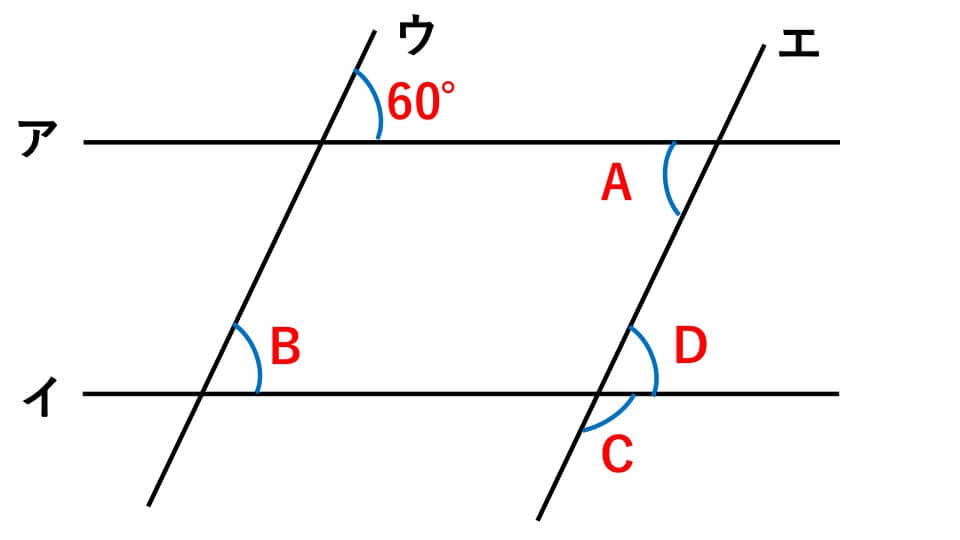



中学受験 算数 角度 基礎からわかりやすくポイント解説 中学受験アンサー



昔 私立の高校入試で見た 角度を求める問題 3つの正方形 Miyayoshiの気まぐれblog




無料の学習プリント 小学4年生の算数ドリル 角度4 総合問題 みそにゃch




中学受験 算数 角度 基礎からわかりやすくポイント解説 中学受験アンサー




数学の対頂角 同位角 錯角 角度が等しい理由 証明まで解説 リョースケ大学



1




関野喬 Twitterissa ファーストインプレッションでは こんな補助線も 直角2つが向かい合っているので 向かい合った2つの角の角度の和が180度 よってabcdは円に内接します B Dは円周角になり 90度ですので Acは円の直径 Acdは条件か直角二等辺三角形 こんな
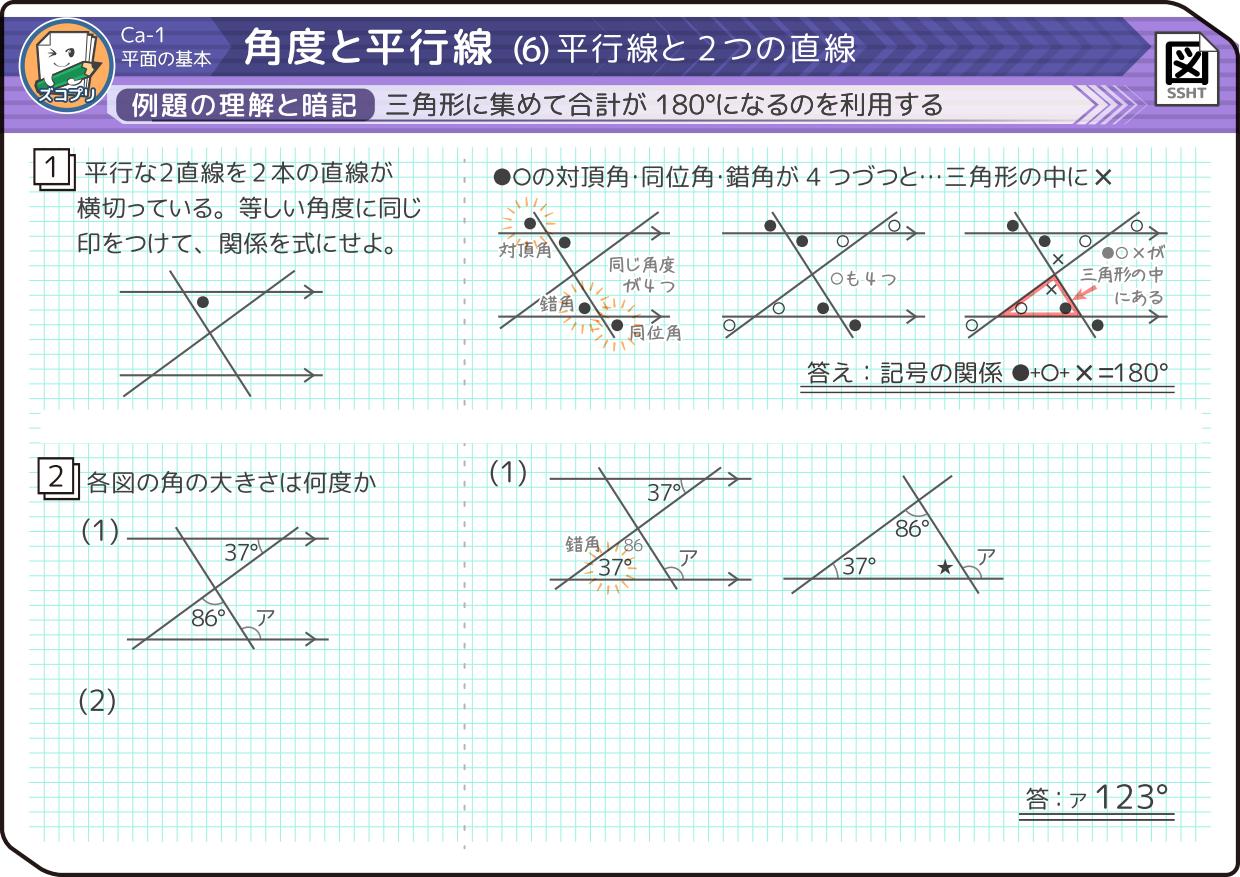



小学4年生 角度の求め方は 対頂角 平行線 同位角 錯角 中学受験 そうちゃ式 受験算数 2号館 図形 速さ



図形の扉 向かい合った角 対頂角



1




あ かまでの角度を求めてください 急いでます 教えてください Clear




三角形の面積の求め方まとめ タイプ別でわかる公式一覧 アタリマエ



2
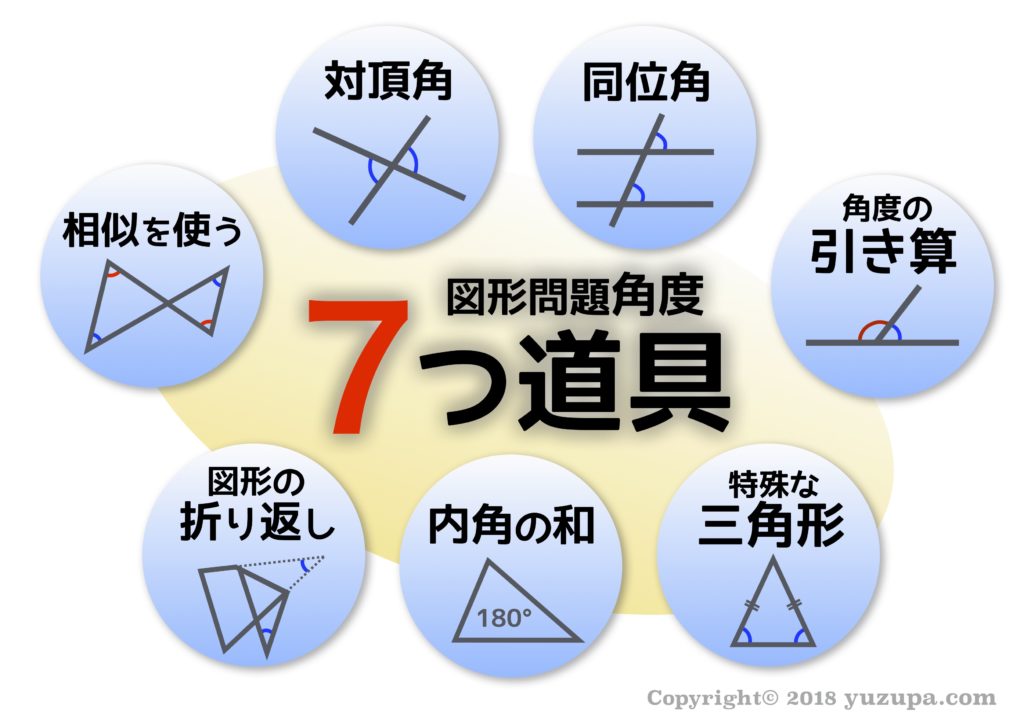



中学受験 図形の角度問題は 7つ道具 で攻略 かるび勉強部屋




対頂角 同位角 錯角の性質と簡単な覚え方 数学fun



中学数学円の中の四角形の向かい合う内角の和は 180度と習ったので Yahoo 知恵袋




数学の対頂角 同位角 錯角 角度が等しい理由 証明まで解説 リョースケ大学




中2 中2数学 平行と合同2 中学生 数学のノート Clear
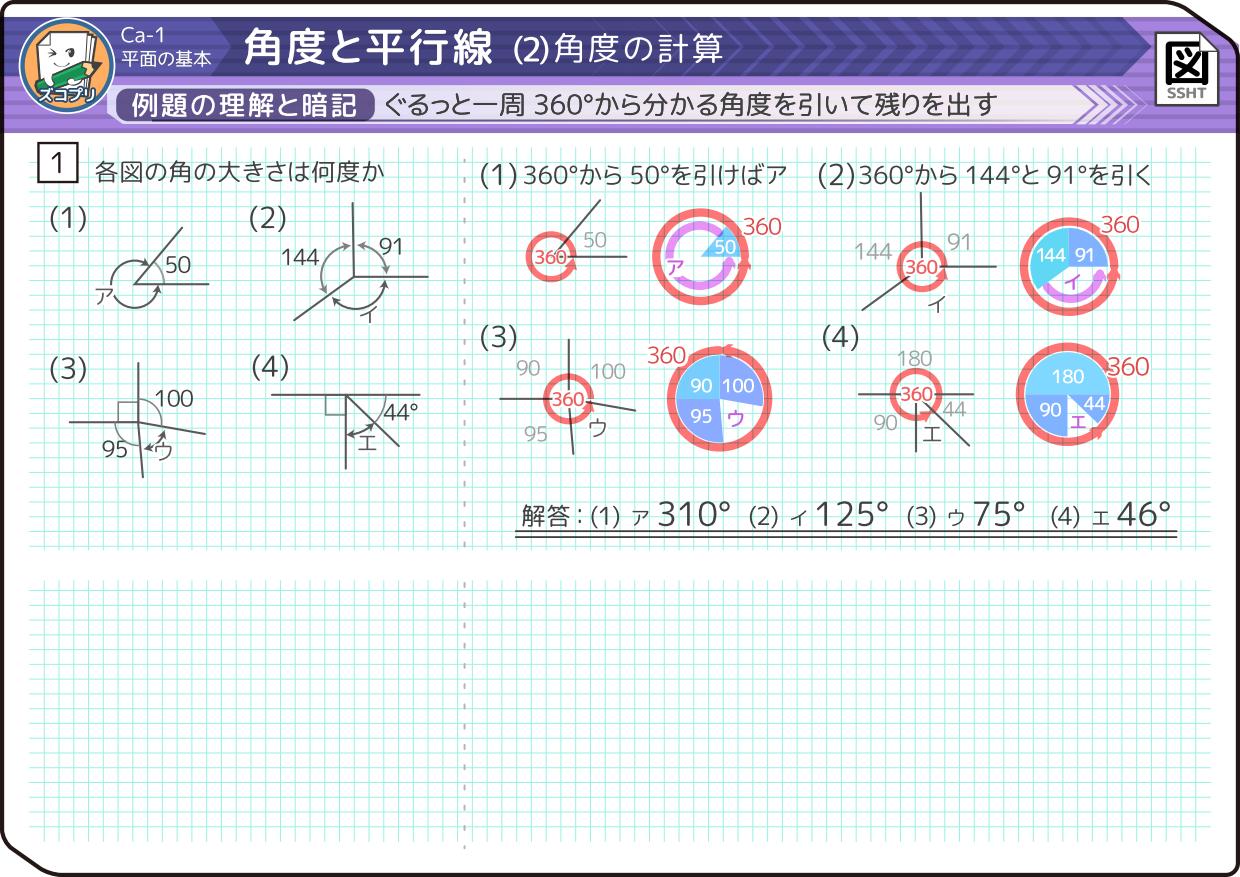



小学4年生 角度の求め方は 対頂角 平行線 同位角 錯角 中学受験 そうちゃ式 受験算数 2号館 図形 速さ



みんなの算数オンライン 教科書レベル 4年 角度 いろいろな四角形 平行な線と角度 平行四辺形 トレーニング
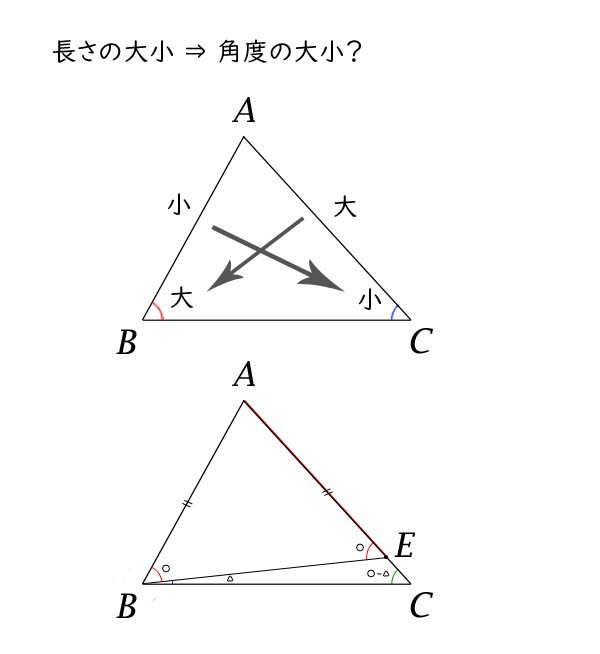



三角形の辺の長さと角の大きさの関係 高校数学マスター



四角形の種類と定義 性質の違い 正方形 長方形 平行四辺形 ひし形 台形 数学fun



中学受験 算数 角度 基礎からわかりやすくポイント解説 中学受験アンサー



ひし形の作図ってどうやるの 宿題のお手伝いに役立つひし形の書き方 小学館hugkum




小学5年生 合同な図形 解説を見ても分かりません みなさん今晩は 数学 教えて Goo




中2 中2数学 平行と合同2 中学生 数学のノート Clear
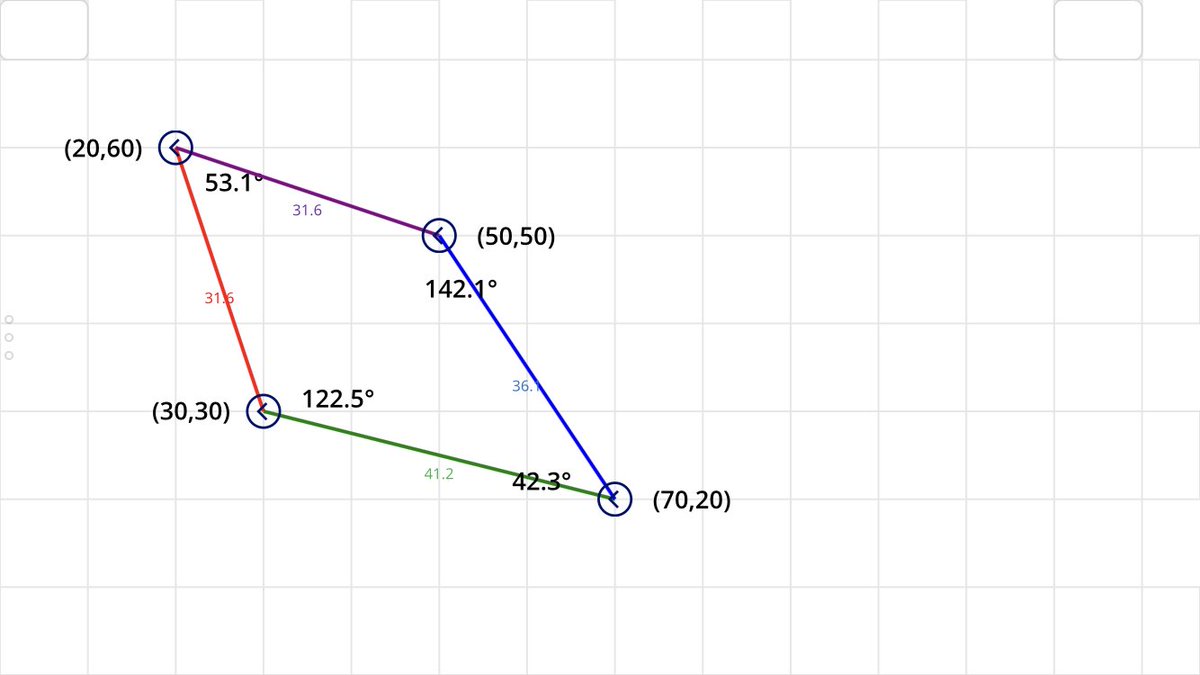



Hiro 四角形の内角の和は常に360です とか 平行四辺形は向かい合う角の角度が一緒で隣り合う角の和は180です みたいな教育に最適じゃないか いいもの作った 自画自賛
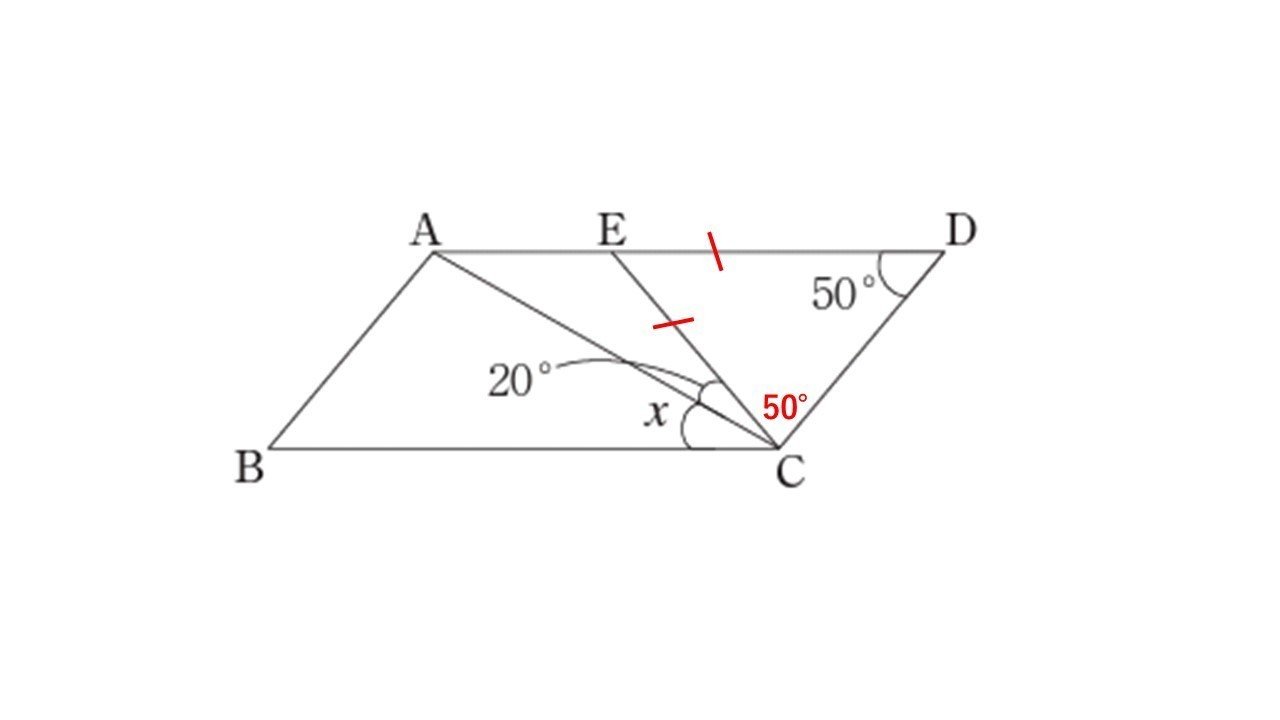



中学数学の平面図形の角度を求める問題を通して学び直しする論理 数学の基礎 タロウ岩井の数学と英語 Note



2



平行四辺形




中学数学 対頂角 同位角 錯角 中学数学の無料オンライン学習サイトchu Su
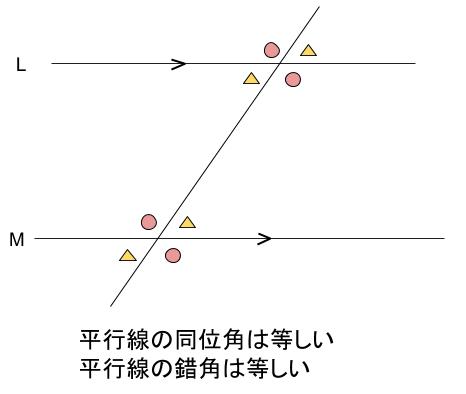



中学数学 対頂角 同位角 錯角 中学数学の無料オンライン学習サイトchu Su




実践記録算数4年




1 Introduction Neutrinos Windows To New Physics Neutrino



数学についての質問です 対角と対頂角は 両方とも同じ意味なので Yahoo 知恵袋




小4算数 Aと同じ角度はどれ 垂直と平行といろいろな四角形 台形 平行四辺形 ひし形 の解き方 教え方 いっしょに勉強しよ



二等辺三角形とは 定義や定理 角度 辺の長さ 面積の求め方 受験辞典



小4算数の問題です 2つの直線が交わってできる4つの角のうち Yahoo 知恵袋
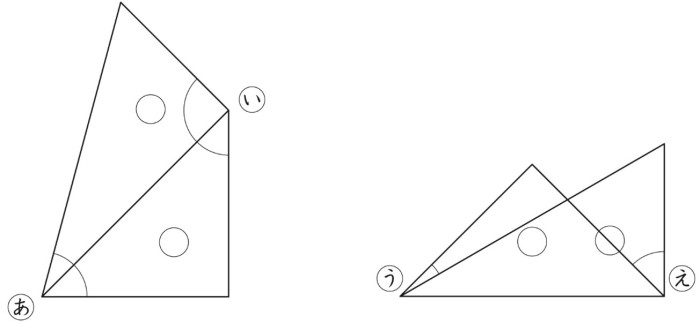



動画で学習 2 角度のはかり方 算数
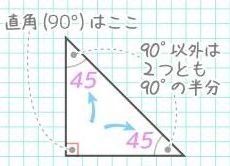



小学4年生 角度の求め方は 対頂角 平行線 同位角 錯角 中学受験 そうちゃ式 受験算数 2号館 図形 速さ




平行線と角 対頂角 錯角 同位角とは 教遊者




Xの角度の求め方を教えてください 3 と 5 です 円周角の問題です Clear



1
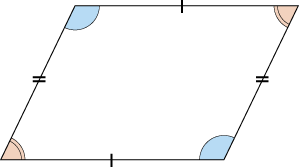



平行四辺形の性質 5年生 算数の広場
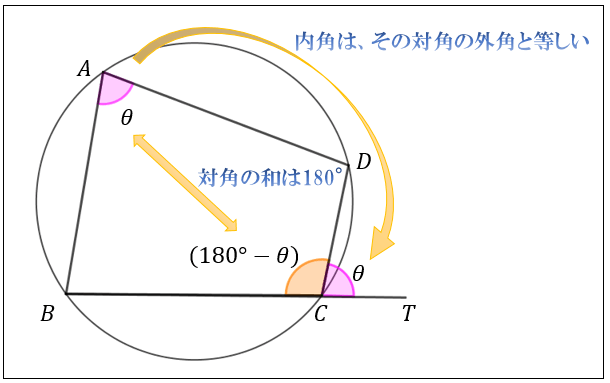



円に内接する四角形の性質まとめ 対角の和が180 になる理由 アタリマエ
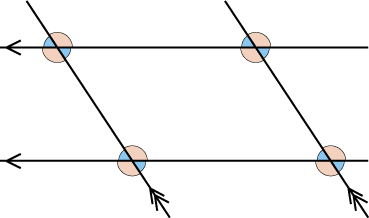



5年生 算数の広場
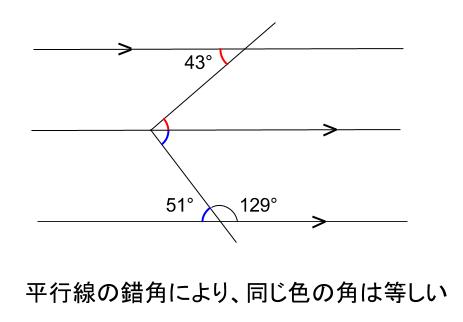



中学数学 対頂角 同位角 錯角 中学数学の無料オンライン学習サイトchu Su
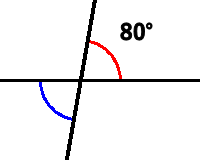



直線と角度



30分でおさらいする小学算数まとめ Orangeprose




算数 小4 9 角の大きさ 三角じょうぎ Youtube
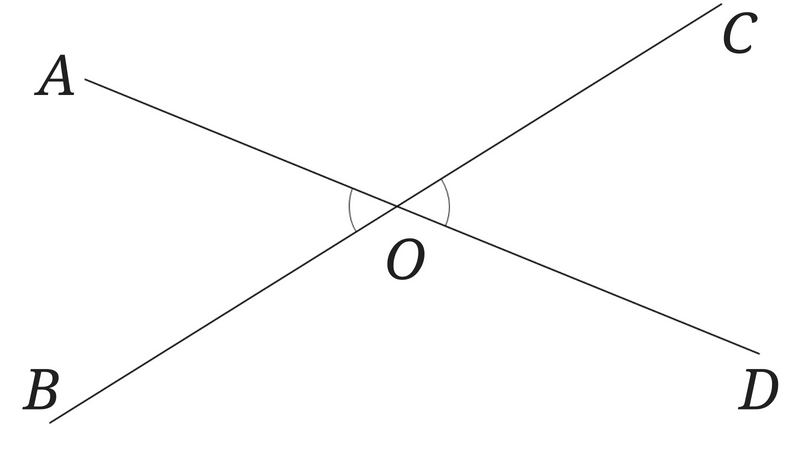



対頂角の性質と大きさが等しい理由は まぜこぜ情報局
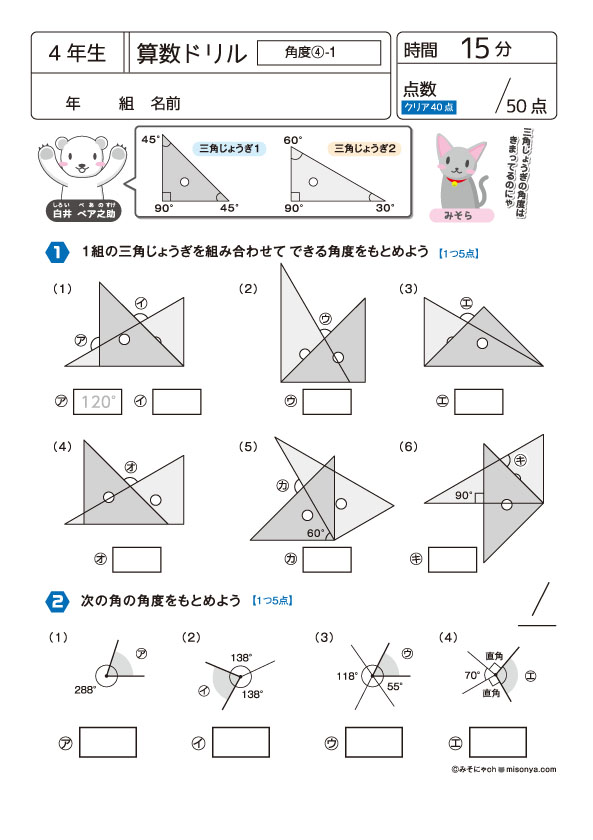



無料の学習プリント 小学4年生の算数ドリル 角度4 総合問題 みそにゃch




中学生 数学 直線が交わるときにできる対頂角 たいちょうかく の性質 おかわりドリル



Q Tbn And9gcrp3lzs2 Tbdgi Wi0twgny6vlfiflc4gm9vfypgdk Usqp Cau




中学受験算数 折り返した図形の角度の問題 Stupedia
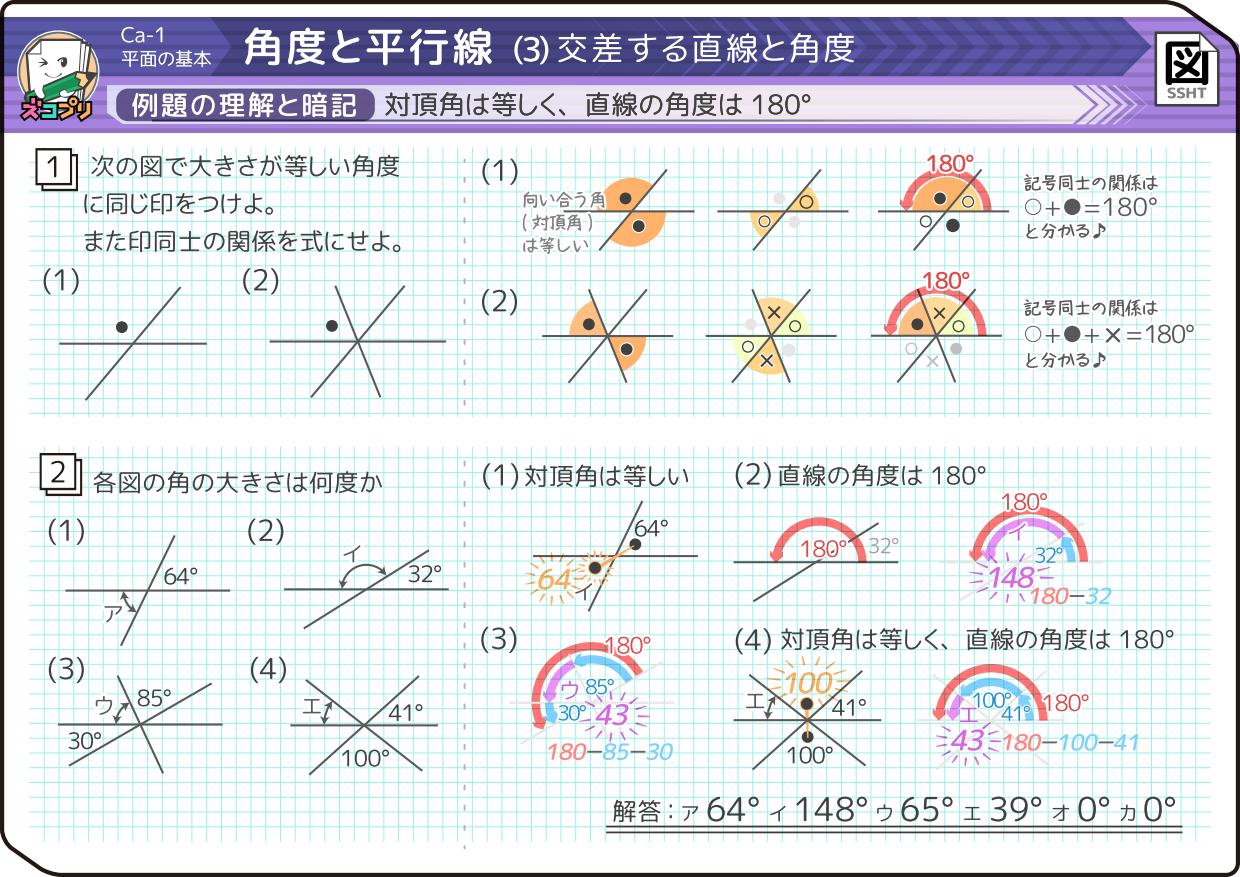



小学4年生 角度の求め方は 対頂角 平行線 同位角 錯角 中学受験 そうちゃ式 受験算数 2号館 図形 速さ
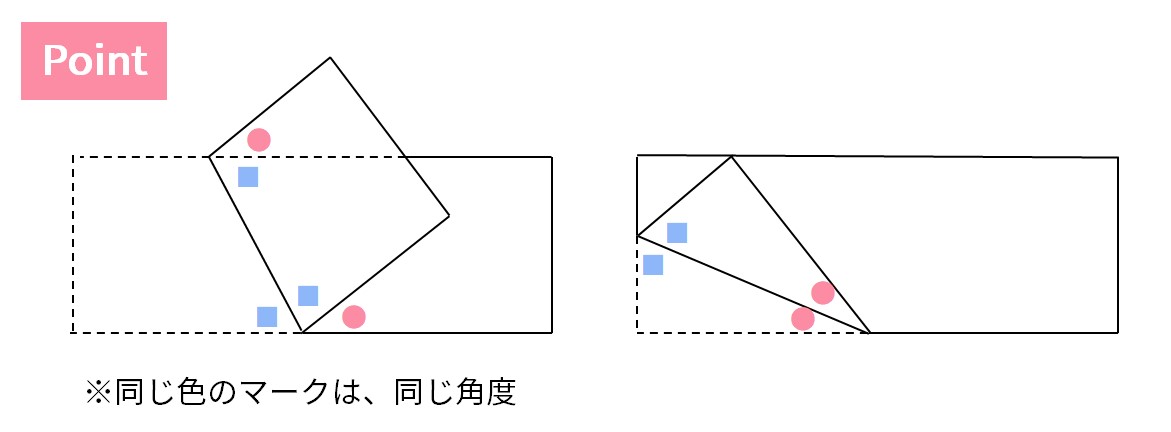



中学受験算数 折り返した図形の角度の問題 Stupedia




台形と平行四辺形の定義 ちがい 小岩 個別指導 元小学校教師が教える個別指導塾 できる子ども育成塾 小岩 篠崎の小学生専門 国語と算数の苦手を克服




平行四辺形の面積を対角線の長さと角度から求める 解説図付き なぜか分かる はかせちゃんの怪しい研究室




小学4年生 角度の求め方は 対頂角 平行線 同位角 錯角 中学受験 そうちゃ式 受験算数 2号館 図形 速さ



中学受験 算数 角度 基礎からわかりやすくポイント解説 中学受験アンサー




数学の対頂角 同位角 錯角 角度が等しい理由 証明まで解説 リョースケ大学




四角形の種類と定義 性質の違い 正方形 長方形 平行四辺形 ひし形 台形 数学fun
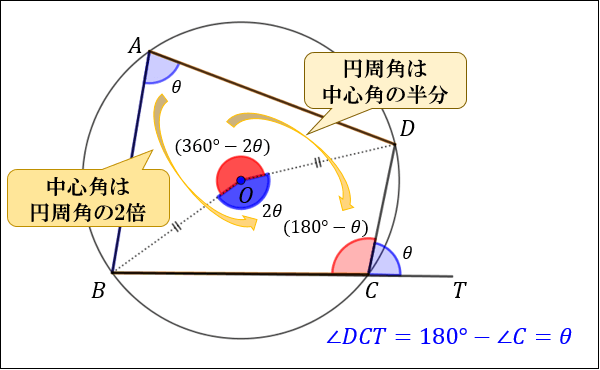



円に内接する四角形の性質まとめ 対角の和が180 になる理由 アタリマエ
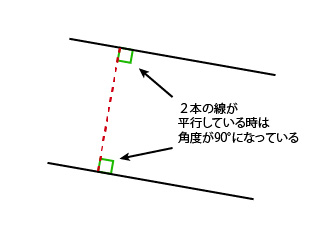



平行四辺形の面積の計算 もう一度やり直しの算数 数学




つまずきをなくす小4 5 6算数平面図形 角度 面積 作図 単位 通販 セブンネットショッピング




円に内接する四角形の性質まとめ 対角の和が180 になる理由 アタリマエ
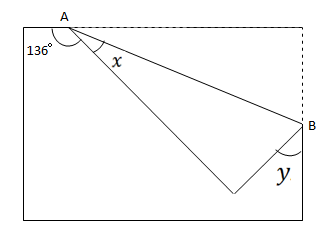



平行線と角度 10 ネット塾
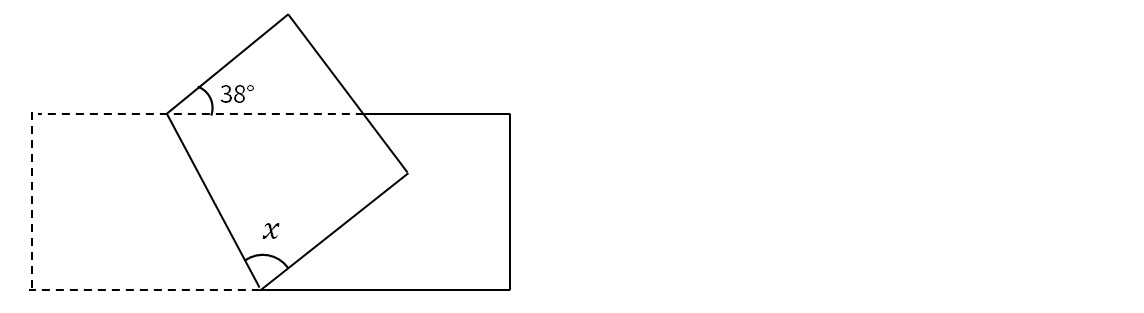



中学受験算数 折り返した図形の角度の問題 Stupedia
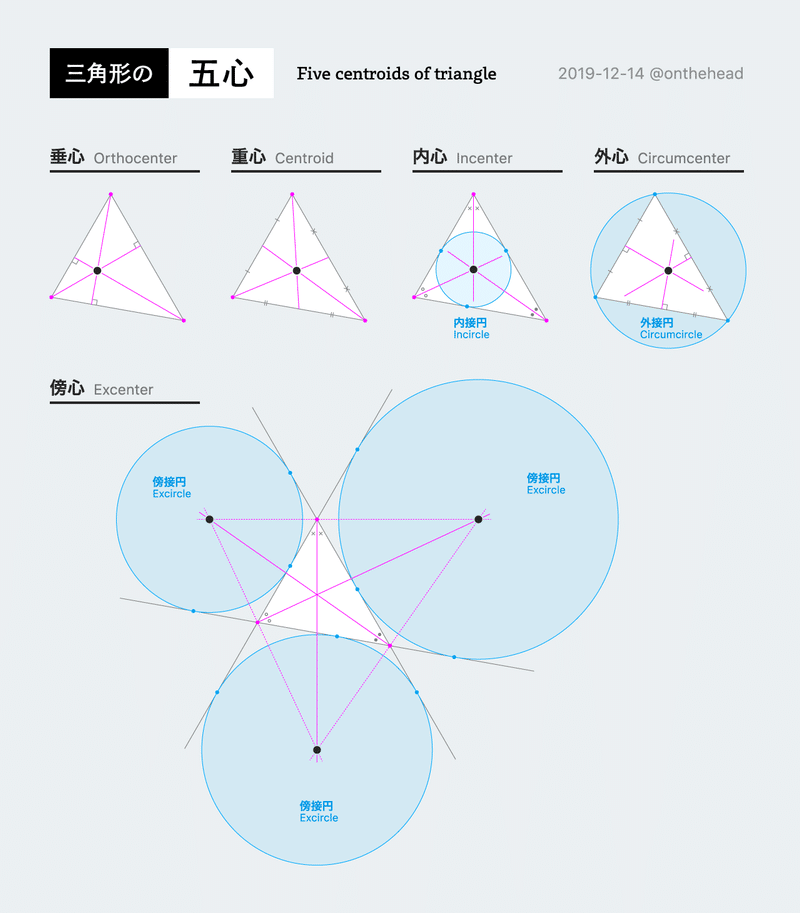



三角形の五心 宮澤聖二 Onthehead Note




角の大きさを計算で求める自主学習ノート例 家庭学習レシピ
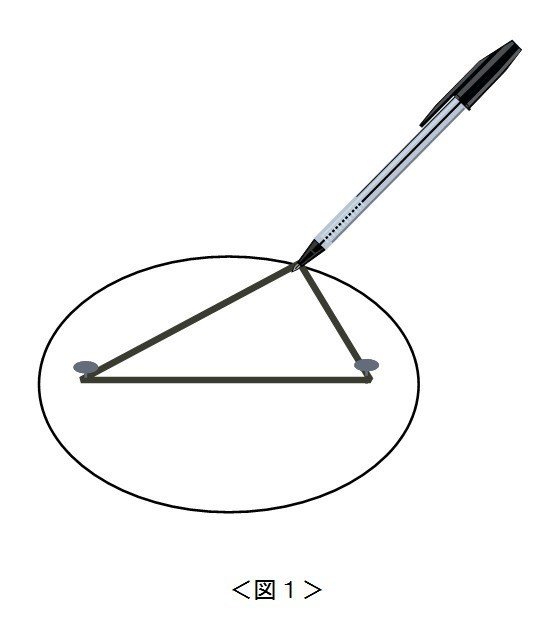



問題 だ円の特徴を考える 川口秀樹 Note



ひし形




中2数学 三角形の合同条件2 2辺とその間の角 練習編 映像授業のtry It トライイット
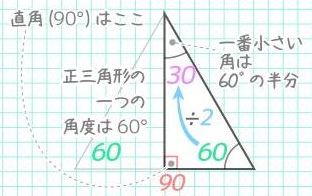



小学4年生 角度の求め方は 対頂角 平行線 同位角 錯角 中学受験 そうちゃ式 受験算数 2号館 図形 速さ




小4 算数 2つの三角じょうぎでできる角度は何度になるの 角度問題の解き方 教え方 いっしょに勉強しよ
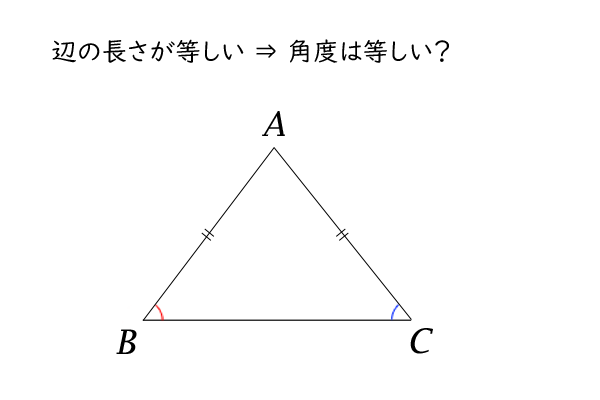



三角形の辺の長さと角の大きさの関係 高校数学マスター



2
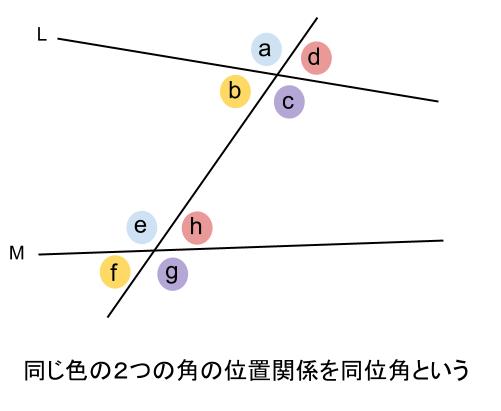



中学数学 対頂角 同位角 錯角 中学数学の無料オンライン学習サイトchu Su
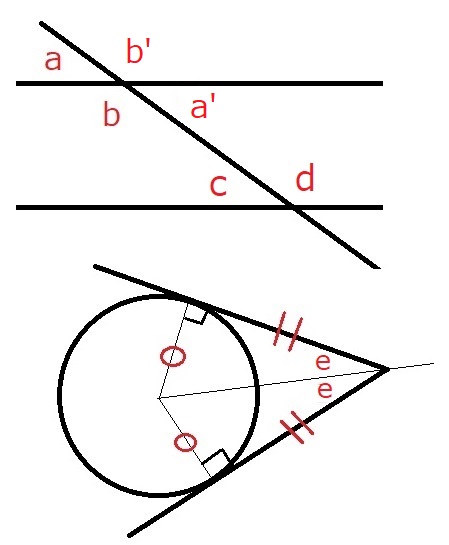



三角関数 機械加工でよく使う計算方法を説明します セドヤのブログ




数学の対頂角 同位角 錯角 角度が等しい理由 証明まで解説 リョースケ大学



図形の問題を得意にしたい
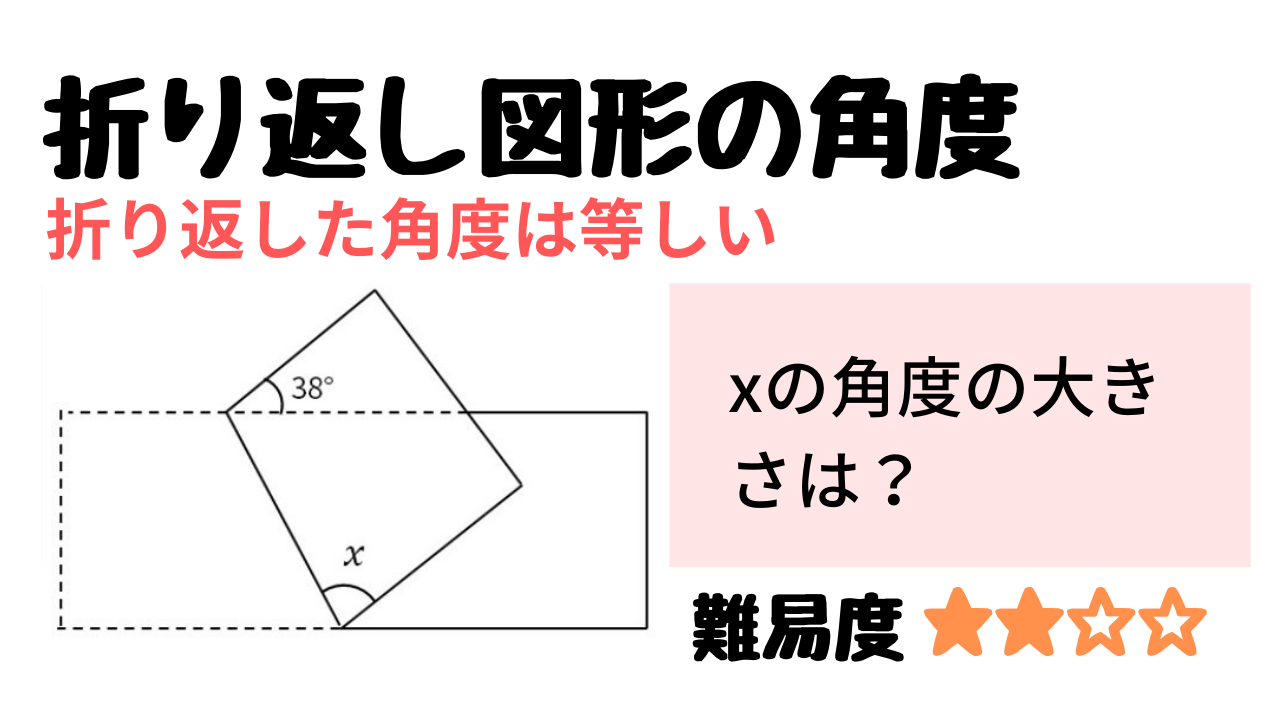



中学受験算数 折り返した図形の角度の問題 Stupedia


